On Inspiration

By Sadaputa Dasa

Copyright © 1981 by Richard L. Thompson

This article was written by my long time friend and colleague from the Bhaktivedanta Institute the late Sadaputa Prabhu, a.k.a. Dr. Richard Thompson, who passed away suddenly in 2008. His death was a great loss to the world of Vaisnavism.

This article On Inspiration is chapter 7 of his book Mechanistic and Non-Mechanistic Science and he refers to other chapters of the book. I heartily recommend this classic, it is well worth the read.

What’s New on This Site

It may be asked why I have included this article on my site? The answer is simple, heighted intuition and inspiration is a must for a Vedic Astrologer or for anyone as seen in the article. It is what separates the mediocre, pedestrian class from the geniuses and masters in any art or science. To understand more about how traditional Vedic astrologers developed their intuition see this article on the Philosophy of Jyotish.

---

In this chapter we will examine how human beings acquire knowledge in science, mathematics, and art. Our focus shall primarily be on the formation of ideas and hypotheses in science and mathematics, since the formal nature of these subjects tends to put the phenomena we are concerned with into particularly clear perspective. We will show that the phenomenon known as inspiration plays an essential part in acquiring knowledge in modern science and mathematics and the creative arts (such as music). We will argue that the phenomenon of inspiration cannot readily be explained by mechanistic models of nature consistent with present-day theories of physics and chemistry.

To give a positive alternative to these models, we will continue the project of outlining the nonmechanistic theoretical system of the Bhagavad-gita. Thus far we have introduced the concept of the conscious self or jivatma as an entity distinct from the material body (Chapters 1 and 2), and we have also introduced the concept of the all-pervading superconscious being or paramatma. The Bhagavad-gita shows how the idea of the paramatma can be used to construct a model of the interaction between the conscious self and the material body. As we shall see, this model accounts for the phenomenon of inspiration in a direct and striking way.

Modern scientists acquire knowledge, at least in principle, by what is called the hypothetico-deductive method. Using this method, they formulate hypotheses and then test them by experimental observation. Investigators consider hypotheses valid only insofar as they are consistent with the data obtained by observation, and they must in principle reject any hypothesis that disagrees with observation. Much analysis has been directed toward the deductive side of the hypothetico-deductive method, but the equally important process of hypothesis formation has been largely neglected. So we ask, “Where do hypotheses come from?”

It is clear that scientists cannot use any direct, step-by-step process to derive hypotheses from raw observational data. To deal with such data at all, they must already have some working hypothesis, for otherwise the data amount to nothing more than a bewildering array of symbols (or sights and sounds), which is no more meaningful than a table of random numbers. In this connection Albert Einstein once said, “It may be heuristically useful to keep in mind what one has observed. But on principle it is quite wrong to try grounding a theory on observable magnitudes alone. In reality the opposite happens. It is the theory which determines what we can observe.”1 Pure mathematics contains an equivalent of the hypothetico-deductive method. In mathematics, instead of hypotheses there are proposed systems of mathematical reasoning intended to answer specific questions. And instead of the experimental testing of a hypothesis there is the step-by-step process of verifying that a particular proof, or line of mathematical reasoning, is correct. This verification process is straightforward and could in principle be carried out by a computer. However, there is no systematic, step-by-step method of generating mathematical proofs and systems of ideas, such as group theory or the theory of Lebesque integration.

Death of Archimedes

If hypotheses in science and systems of reasoning in mathematics are not generated by any systematic procedure, then what is their source? We find that they almost universally arise within the mind of the investigator by sudden inspiration. The classic example is Archimedes’ discovery of the principle of specific gravity. The Greek mathematician was faced with the task of determining whether a king’s crown was solid gold without drilling any holes in it. After a long period of fruitless endeavor, he received the answer to the problem by sudden inspiration while taking a bath.

Such inspirations generally occur suddenly and unexpectedly to persons who had previously made some unsuccessful conscious effort to solve the problem in question. They usually occur when one is not consciously thinking about the problem, and they often indicate an entirely new way of looking at it — a way the investigator had never even considered during his conscious efforts to find a solution. Generally, an inspiration appears as a sudden awareness of the problem's solution, accompanied by the conviction that the solution is correct and final. One perceives the solution in its entirety, though it may be quite long and complicated when written out in full.

Inspiration plays a striking and essential role in the solution of difficult problems in science and mathematics. Generally, investigators can successfully tackle only routine problems by conscious endeavor alone. Significant advances in science almost always involve sudden inspiration, as the lives of great scientists and mathematicians amply attest. A typical example is the experience of the nineteenth century mathematician Karl Gauss. After trying unsuccessfully for years to prove a certain theorem about whole numbers, Gauss suddenly became aware of the solution. He described his experience as follows: “Finally, two days ago I succeeded . . . Like a sudden flash of lightning, the riddle happened to be solved. I myself cannot say what was the conducting thread which connected what I previously knew with what made my success possible.”2

Karl Gauss, 1840, portrait by Jensen.

We can easily cite many similar examples of sudden inspiration. Here is another one, given by Henri Poincaré, a famous French mathematician of the late nineteenth century. After working for some time on certain problems in the theory of functions, Poincaré had occasion to go on a geological field trip, during which he set aside his mathematical work. While on the trip he received a sudden inspiration involving his researches, which he described as follows: “At the moment when I put my foot on the step the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used . . . were identical with those of non-Euclidean geometry.”3 Later on, after some fruitless work on an apparently unrelated question, he suddenly realized, “with just the same characteristics of brevity, suddenness, and immediate certainty,”4 that this work could be combined with his previous inspiration to provide a significant advance in his research on the theory of functions. Then a third sudden inspiration provided him with the final argument he needed to complete that work.

Although inspirations generally occur after a considerable period of intense but unsuccessful effort to consciously solve a problem, this is not always the case. Here is an example from another field of endeavor. Wolfgang Mozart once described how he created his musical works: “When I feel well and in good humor, or when I am taking a drive or walking, . . . thoughts crowd into my mind as easily as you could wish. Whence and how do they come? I do not know and I have nothing to do with it . . . Once I have a theme, another melody comes, linking itself with the first one, in accordance with the needs of the composition as a whole . . . Then my soul is on fire with inspiration, if however nothing occurs to distract my attention. The work grows; I keep expanding it, conceiving it more and more clearly until I have the entire composition finished in my head, though it may be long . . . It does not come to me successively, with its various parts worked out in detail, as they will be later on, but it is in its entirety that my imagination lets me hear it."5 (Italics added. )

From these instances we discover two significant features of the phenomenon of inspiration: first, its source lies beyond the subject’s conscious perception; and second, it provides the subject with information unobtainable by any conscious effort. These features led Poincaré and his follower Hadamard to attribute inspiration to the action of an entity which Poincaré called the “subliminal self,” and which he identified with the subconscious or unconscious self of the psychoanalysts. Poincaré made the following interesting observations about the subliminal self: “The subliminal self is in no way inferior to the conscious self; it is not purely automatic; it is capable of discernment; it has tact, delicacy; it knows how to choose, to divine. What do I say? It knows better how to divine than the conscious self, since it succeeds where that has failed. In a word, is not the subliminal self superior to the conscious self?”6 Having raised this question, Poincaré then backs away from it: “Is this affirmative answer forced upon us by the facts I have just given? I confess that for my part, I should hate to accept it.”7 He then offers a mechanical explanation of how the subliminal self, viewed as an automaton, could account for the observed phenomena of inspiration.

7.1 The Mechanistic Explanation

Let us carefully examine the arguments for such a mechanical explanation of inspiration. This issue is of particular importance at the present time, because the prevailing materialistic philosophy of modern science holds that the mind is nothing more than a machine, and that all mental phenomena, including consciousness, are nothing more than the products of mechanical interactions. The mental machine is specifically taken to be the brain, and its basic functional elements are believed to be the nerve cells and possibly some systems of interacting macromolecules within these cells. Many modern scientists believe that all brain activity results simply from the interaction of these elements according to the known laws of physics.

No scientist has yet formulated an adequate explanation of the difference between a conscious and an unconscious machine, or even indicated how a machine could be conscious at all. In fact, investigators attempting to describe the self in mechanistic terms concentrate exclusively on the duplication of external behavior by mechanical means; they totally disregard the individual person’s subjective experience of conscious self-awareness. (See Chapter 2. ) This approach to the self is characteristic of modern behavioral psychology. It was formally set forth by the British mathematician Alan Turing, who argued that since whatever a human being can do a computer can imitate, a human being is merely a machine.

For the moment we will follow this behavioristic approach and simply consider the question of how the phenomenon of inspiration could be duplicated by a machine. Poincaré proposed that the subliminal self must put together many combinations of mathematical symbols by chance until at last it finds a combination satisfying the desire of the conscious mind for a certain kind of mathematical result. He proposed that the conscious mind would remain unaware of the many useless and illogical combinations running through the subconscious, but that it would immediately become aware of a satisfactory combination as soon as it was formed. He therefore proposed that the subliminal self must be able to form enormous numbers of combinations in a short time, and that these could be evaluated subconsciously as they were formed, in accordance with the criteria for a satisfactory solution determined by the conscious mind.

As a first step in evaluating this model, let us estimate the number of combinations of symbols that could be generated within the brain within a reasonable period of time. A very generous upper limit on this number is given by the figure 3.2 x 10⁴⁶. We obtain this figure by assuming that in each cubic Ångstrom unit of the brain, a separate combination is formed and evaluated once during each billionth of a second over a period of one hundred years. Although this figure is an enormous overestimate of what the brain could possibly do within the bounds of our present understanding of the laws of nature, it is still infinitesimal compared to the total number of possible combinations of symbols one would have to form to have any chance of randomly hitting a proof for a particular mathematical theorem of moderate difficulty.

If we attempt to elaborate a line of mathematical reasoning, we find that at each step there are many possible combinations of symbols we can write down, and thus we can think of a particular mathematical argument as a path through a tree possessing many successive levels of subdividing branches. This is illustrated in the figure below. The number of branches in such a tree grows exponentially with the number of successive choices, and the number of choices is roughly proportional to the length of the argument. Thus as the length of the argument increases, the number of branches will very quickly pass such limits as 10⁴⁶ and 10¹⁰⁰ For example, suppose we are writing sentences in some symbolic language, and the rules of grammar for that language allow us an average of two choices for each successive symbol. Then there will be approximately l0¹⁰⁰ grammatical sentences of 333 symbols in length.

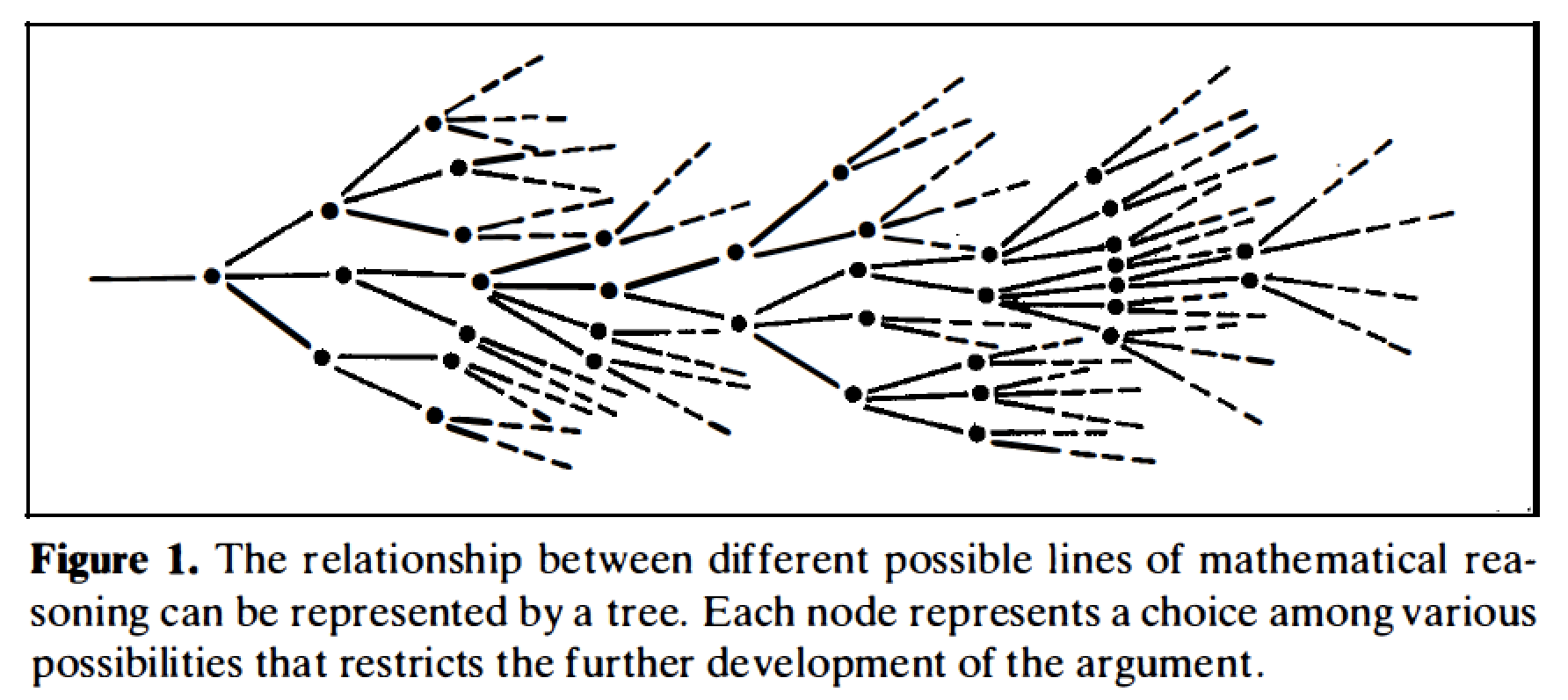
Even a very brief mathematical argument will often expand to great length when written out in full, and many mathematical proofs require pages and pages of highly condensed exposition, in which many essential steps are left for the reader to fill in. Thus there is only an extremely remote chance that an appropriate argument would appear as a random combination in Poincaré’s mechanical model of the process of inspiration. Clearly, the phenomenon of inspiration requires a process of choice capable of going more or less directly to the solution, without even considering the vast majority of possible combinations of arguments.

7.2 Some Striking Examples

The requirements that this process of choice must meet are strikingly illustrated by some further examples of mathematical inspiration. It is very often found that the solution to a difficult mathematical problem depends on the discovery of basic principles and underlying systems of mathematical relationships. Only when these principles and systems are understood does the problem take on a tractable form. Therefore difficult problems have often remained unsolved for many years, until mathematicians gradually developed various sophisticated ideas and methods of argument that made their solution possible. However, it is interesting to note that on some occasions sudden inspiration has completely circumvented this gradual process of development. There are several instances in which famous mathematicians have, without proof, stated mathematical results that later investigators proved only after elaborate systems of underlying relationships had gradually come to light. Here are two examples:

The first example concerns the zeta-function studied by the German mathematician Bernhard Riemann. At the time of his death, Riemann left a note describing several properties of this function that pertain to the theory of prime numbers. He did not give any proof for existence of these properties, and many years elapsed before mathematicians were able to find existence proofs for all but one of them. The remaining question is still unsettled, though an immense amount of labor has been devoted to it over the last seventy-five years. Of the properties of the zeta-function that have been verified, the mathematician Jacques Hadamard said, “All these complements could be brought to Riemann’s publication only by the help of facts which were completely unknown in his time; and, for one of the properties enunciated by him, it is hardly conceivable how he can have found it without using some of these general principles, no mention of which is made in his paper.”8

The work of the French mathematician Evariste Galois provides us with a case similar to Riemann's. Galois is famous for a paper, written hurriedly in sketchy form just before his death, that completely revolutionized the subject of algebra. However, the example we are considering here concerns a theorem Galois stated, without proof, in a letter to a friend. According to Hadamard this theorem could not even be understood in terms of the mathematical knowledge of that time; it became comprehensible only years later, after the discovery of certain basic principles. Hadamard remarks "(1) that Galois must have conceived these principles in some way; (2) that they must have been unconscious in his mind, since he makes no allusion to them, though they themselves represent a significant discovery.”9

It would appear, then, that the process of choice underlying mathematical inspiration can make use of basic principles that are very elaborate and sophisticated and that are completely unknown to the conscious mind of the person involved. Some of the developments leading to the proof of Riemann's theorems are highly complex, requiring many pages (and even volumes) of highly abbreviated mathematical exposition. It is certainly hard to see how a mechanical process of trial and error, such as that described by Poincaré, could exploit such principles. Yet, if other, simpler solutions exist that avoid the use of such elaborate developments, they have remained unknown up to the present time, despite the extensive research devoted to these topics.

The process of choice underlying mathematical inspiration must also make use of selection criteria that are exceedingly subtle and hard to define. Mathematical work of high quality cannot be evaluated simply by the application of cut-and-dried rules of logic. Rather, its evaluation involves emotional sensibility and the appreciation of beauty, harmony, and other delicate aesthetic qualities. Of these criteria Poincaré said, “It is almost impossible to state them precisely ; they are felt rather than formulated .”10 This is also true of the criteria by which we judge artistic creations, such as musical compositions. These criteria are very real but at the same time very difficult to define precisely. Yet evidently they were fully incorporated in that mysterious process which provided Mozart with sophisticated musical compositions without any particular effort on his part and, indeed, without any knowledge on his part of how it was all happening.

If the process underlying inspiration is not one of extensive trial and error, as Poincaré suggested, but rather one that depends mainly on direct choice, then we can explain it in terms of current mechanistic ideas only by positing the existence of a very powerful algorithm (a system of computational rules) built into the neural circuitry of the brain. However, it is not at all clear that we can satisfactorily explain inspiration by reference to such an algorithm. Here we will briefly discuss two major problems entailed by the brain-algorithm hypothesis.

(1) Origins. If mathematical, scientific, and artistic inspirations result from the workings of a neural algorithm, then how does the pattern of nerve connections embodying this algorithm arise? We know that the algorithm cannot be a simple one when we consider the complexity of the automatic theorem-proving algorithms that have been produced thus far by workers in the field of artificial intelligence.11 These algorithms cannot even approach the performance of advanced human minds, and yet they are extremely elaborate. But if our hypothetical brain-algorithm is extremely complex, how did it come into being? It can hardly be accounted for by extensive random genetic mutation or recombination in a single generation, for then the problem of random choice among vast numbers of possible combinations would again arise. One would therefore have to suppose that only a few relatively probable genetic transformations separated the genotype of Mozart from those of his parents, who, though talented, did not possess comparable musical ability.

However, it is not the usual experience of those who work with algorithms that a few substitutions or recombinations of symbols can drastically improve an algorithm's performance or give it completely new capacities that would impress us as remarkable. Normally, if this were to happen with a particular algorithm, we would tend to suppose that it was a defective version of another algorithm originally designed to exhibit those capacities. This would imply that the algorithm for Mozart's unique musical abilities existed in a hidden form in the genes of his ancestors.

This brings us to the general problem of explaining the origin of human traits. According to the theory most widely accepted today, these traits were selected on the basis of the relative reproductive advantage they conferred on their possessors or their possessors’ relatives. Most of the selection for our hypothetical hidden algorithms must have occurred in very early times, because of both the complexity of these algorithms and the fact that they often must be carried in a hidden form. It is now thought that human society, during most of its existence, was on the level of hunters and gatherers, at best. It is quite hard to see how, in such societies , persons like Mozart or Gauss would ever have had the opportunity to fully exhibit their unusual abilities. But if they didn’t, then the winnowing process posited by the theory of evolution could not effectively select these abilities.

We are thus faced with a dilemma: It appears that it is as difficult to account for the origin of our hypothetical inspiration-generating algorithms as it is to account for the inspirations themselves.

Henri Poincaré

(2) Subjective experience. If the phenomenon of inspiration is caused by the working of a neural algorithm , then why is it that an inspiration tends to occur as an abrupt realization of a complete solution, without the subject’s conscious awareness of intermediate steps? The examples of Riemann and Galois show that some persons have obtained results in an apparently direct way, while others were able to verify these results only through a laborious process involving many intermediate stages. Normally, we solve relatively easy problems by a conscious, step-by-step process. Why, then, should inspired scientists, mathematicians, and artists remain unaware of important intermediate steps in the process of solving difficult problems or producing intricate works of art, and then become aware of the final solution or creation only during a brief experience of realization?

Thus we can see that the phenomenon of inspiration cannot readily be explained by means of mechanistic models of life consistent with present day theories of physics and chemistry. In the remainder of this chapter we will explore the nonmechanistic approach of the Bhagavad-gita.

7.3 The Interaction Between
Consciousness and Matter

In the first part of this book we discussed consciousness and, drawing from the Bhagavad-gita. introduced the conception of the conscious self as a nonphysical entity. In the second part we discussed biological form and the problem of finding a unified description of nature. We concluded that it is not possible to construct a unified quantitative theory that can give a satisfactory account of the origin of complex forms, such as the bodily structures of living organisms. But turning once again to the Bhagavad-gita, we showed how an intuitively reasonable, unified picture of nature can be based on the nonquantifiable idea of universal consciousness.

Thus far we have not given any indication of how the conscious self, or jivatma influences the behavior of the material body. As we observed in Chapter 2, philosophers have not been able to solve this problem, and many have responded either by denying the existence of consciousness or by trying to explain it as a byproduct of brain activity. Nonetheless, a simple solution does exist. The Bhagavad-gita indicates that the interplay between the conscious self and the material body is indirect. and depends on the interaction between the localized self and universal consciousness. This explanation of the relationship between the jivatma and matter resolves many of the problems that have perplexed philosophers, and it also directly accounts for the phenomena of inspiration. Most importantly, this explanation entails a direct method of obtaining verifiable knowledge about both localized and universal consciousness.

The description of the interaction between the jivtatma and the material body given in the first part of the Bhagavad-gita may seem perplexing: “The bewildered spirit soul, under the influence of the three modes of material nature, thinks himself to be the doer of activities, which are in actuality carried out by nature.”12 Or again: “The embodied spirit, master of the city of his body, does not create activities, nor does he influence people to act, nor does he create the fruits of action. All this is enacted by the modes of material nature.”13 Apparently, these statements support the viewpoint that nature is working entirely in accordance with certain fixed laws, and that the conscious self can at best be an epiphenomenon affected by the actions of the material body but unable to affect them in turn.

The Bhagavad-gita confirms that nature is indeed working according to laws. But the key to the solution of the mind-body problem lies in understanding the character of these laws. Physicists tend to conceive of the laws of nature as a closed set of immutable rules that can be specified by a few simple equations. According to the Bhagavad-gita, however, the laws of nature are like the laws of human society promulgated by a head of state. Like the laws of the physicists, these laws can also be represented in symbolic terms, but unlike them they tend to be highly complex. And since the laws of nature are actually under personal control, they are always subject to interference and modification.

In the Bhagavad-gita the Supreme Person, Krsna, describes the laws of nature in the following terms: “This material nature is working under My direction, O son of Kunti, and it is producing all moving and nonmoving beings. By its rule this manifestation is created and annihilated again and again.”14 Thus although the physicists are right that the material energy is acting according to rules, they fail to see that these rules have their ultimate source in a personal director.

We can visualize these rules in terms of a hierarchy. On the lowest level are the relatively simple laws governing the gross behavior of matter. These are studied to some extent by physicists and chemists. On the next level are higher-order laws governing the complex behavior of the living beings. These laws, sometimes referred to as the laws of karma (action), are discussed in the Bhagavad-gita in some detail. Finally, on the highest level are the direct interventions of the Supreme Person in the course of natural events. We have discussed in Parts I and II how one can extend the world view of modern science to encompass such an open-ended hierarchy of natural laws. In such a hierarchy the laws on each level are not, of course, absolute. They are merely approximations subject to refinement and modification in accordance with higher laws and, ultimately, the unconstrained will of the Supreme Person.

From the mechanistic viewpoint, such an “unconstrained will” is at best nothing more than a name for the arbitrary and the inexplicable. Yet the Bhagavad-gita describes some additional nonquantifiable factors that can give us greater insight into the will of the Supreme Person. One of these factors is the personal interaction between the Supreme and the localized conscious selves.

In the Bhagavad-gita Krsna states, “The Supreme Lord is situated in Everyone’s heart, 0 Arjuna, and is directing the wanderings of all living entities, who are situated on a machine made of the material energy.”15 As we have already mentioned, the materially embodied jivatma is in an essentially passive state, unable directly to influence the actions of the material body. Yet the jivatma is conscious of the bodily situation and filled with desires relating to the outcome of various bodily activities. According to the Bhagavad-gita, the Supreme Person perceives the desires of the embodied beings and responds to these desires by appropriately controlling the bodily machinery.

The manifestation of the Supreme Person within the heart of every living being is known as the paramatma, or Supersoul . “Although the Supersoul appears to be divided,” says the Bhagavad-gita, “He is never divided. He is situated as one.”16 This is another illustration of the simultaneous oneness and multiplicity of the Supreme Person, which we discussed in Chapter 6. Since the Supreme Person possesses unlimited consciousness, He is able to attend simultaneously to innumerable material situations without becoming confused.

The Supreme Person, as understood from the Bhagavad-gita, is not remote from the material world. Rather, He is all-pervading in space and time and is also transcendental to space and time. This idea may seem paradoxical, but we should note that a similar problem arises when we try to visualize the reality underlying the laws of nature as conceived in modern physics. These laws are postulated as spatially and temporally invariant; but what is it that pervades all space and time and determines that gravitation, for example, will operate according to a certain universal force constant, G?

In our day-to-day experience we desire to perform various physical actions, and we generally find that the body immediately acts in accordance with our desires. Although we do not understand how our will gives rise to action, this seems to happen automatically, and we normally take it for granted and think, “I am doing this.” According to the Bhagavad-gita, what is actually happening is that the Supersoul is perceiving our desires and translating them into action . He does this through the manipulation of the laws of nature on a sophisticated level. As a consequence, our actions seem to conform to the known physical laws, even though, if we could analyze these actions thoroughly enough, we would find no fixed system of laws ultimately able to account for them.

Krsna as the Paramatma in the heart of all living entities

The philosophy of the Bhagavad-gita thus provides us with a simple explanation of the phenomenon of inspiration — the very explanation , alas, that Poincaré, after analyzing his own mathematical inspirations, felt he would hate to accept. In each of the cases we have discussed, a person initially desired very strongly to carry out a difficult mental task, such as finding the proof of a mathematical theorem. Generally, the person spent some time fruitlessly endeavoring to execute the task , and then he suddenly and unexpectedly became aware of the solution to his problem . (The example of Mozart shows, however, that an initial period of frustrating failure is not always involved.) We have seen that in many instances such unexpected realizations cannot be satisfactorily explained as byproducts of known physical processes. But we can readily understand experiences of sudden illumination as the responses of the Supersoul to the desires of the embodied living being.

We should note that different persons will generally have different experiences of inspiration. Even if two people desiring to solve the same problem are of similar ability and education, one may find the solution and the other may not. The Bhagavad-gita explains this variance as a consequence of karma, or the accumulated byproducts of past actions. The Supersoul does not direct the actions of the material body solely in accordance with the immediate desires of the living being. Rather, He determines these actions by systematically evaluating both the living being’s current desires and his past activities. He bases these judgments on an established set of higher-order laws-the laws of karma-which provide an absolute standard for universal justice and morality. These laws are just as real as the “natural laws” of physics and chemistry. But they are much more complex than these laws, and they are directly involved with the phenomenon of life.

The Bhagavad-gita deals primarily with the means whereby the individual conscious being can become free from the bondage of past karma. A living being acting under the laws of karma is more or less a helpless spectator of an elaborate drama of actions and reactions stemming from past and present desires. In this state the living being tends to identify fully with his physical body and to be completely unaware of the role played by the Supersoul in the affairs of his life.

Under the laws of karma, the relationship between the individual jivatma and the Supreme Person is essentially impersonal and legalistic. Yet it is possible for the jivatma to become directly aware of the Supreme Person and reciprocate with Him in a personal relationship. In such a state of consciousness, the jivatma is freed from karmic reactions to past activities and becomes fully aware of his own nature as a nonphysical being.

Inspiration plays an essential role in the attainment of this state of consciousness. In the Bhagavad-gita Krsna declares, “To those who are constantly devoted and worship Me with love, I give the understanding by which they can come to Me . Out of compassion for them, I dwelling in their hearts, destroy with the shining lamp of knowledge the darkness born of ignorance.”17 The purport of this statement is that direct knowledge of the Supreme Person is available to any person willing to approach the Supreme with a positive, favorable attitude. Normally, Krsna supplies the embodied jivatma only with information relating to his particular material desires, but if the jivatma approaches Krsna with love and without underlying material motives, then Krsna will directly reveal Himself.

This is the conclusion of the Bhagavad-gita’s philosophy, and it constitutes the only real means of verifying the truth of this philosophy. By analyzing empirical arguments, we can identify some of the shortcomings of mechanistic theories and show how the philosophy of the Bhagavad-gita can supply important elements now missing from the prevailing scientific world view. But if we remain within the framework of mechanistic thought, we can neither prove that this philosophy is true nor practically apply it. We can verify transcendental subject matter only if we are able to actually function on the transcendental platform.

In the discussion thus far we have indicated that according to the Bhagavad-gita, such transcendental consciousness is theoretically attainable. The individual self is always in contact with the Supersoul and is capable, in principle, of relating with the Supersoul on the level of direct personal exchange. In Chapter 9 we will discuss the epistemology of transcendental knowledge and indicate briefly how this theoretical possibility might be practically realized.

Subscribe to our mailing list. And get our intermittent newsletter and updates to this site.

Notes

l. Brush, “Should the History of Science be Rated X?” p. 1167. ↩

2. Hadamard , The Psychology of Invention in the Mathematical Field, p. 15. ↩

3. Poincaré, The Foundations of Science, pp. 387-388. ↩

4. Ibid. ↩

5. Hadamard, p. 16.↩

6. Poincaré, p. 390.↩

7. Poincaré, p. 391.↩

8. Hadamard, p. 118.↩

9. Hadamard, p. 120.↩

10. Poincaré, p. 390.↩

11. Weizenbaum, Computer Power and Human Reason, chap. 9.↩

12. A. C. Bhaktivedanta Swami Prabhupada, Bhagavad-gita As It Is, text 3.27, p. 192.↩

13. Ibid., text 5.14, p. 286.↩

14. Ibid., text 9.10, p. 457.↩

15. Ibid., text 18.61, p. 830.↩

16. Ibid., text 13.17, p. 640.↩

17. Ibid., texts 10.10-11, pp. 506-508.↩

References

Bhaktivedanta Swami Prabhupada, A. C. Bhagavad-gita As It Is. Sanskrit text, translation, and commentary. New York: Collier Books, 1972.

Brush, Stephen G. “Should the History of Science be Rated X?” Science. Vol. 183, 22 March 1974, pp. 1164-1172.

Hadamard, Jacques. The Psychology of Invention in the Mathematical Field. Princeton: Princeton University Press, 1949.

Poincaré, Henri. The Foundations of Science. Lancaster, Pa. : The Science Press, 1946.

Weizenbaum, Joseph. Computer Power and Human Reason. San Francisco: W. H. Freeman and Co., 1976.